The Mathematics of The Walking Dead

The popular zombie drama, The Walking Dead, has elapsed over a time of about 2 years. But this simple calculation shows that the surviving humans should have killed all the zombies long before that time had elapsed. Let's take a closer look considering infection rates, birth, and death rates and see how those affect the population of zombies vs. humans over time. What do these rates have to be for the zombie apocalypse to stretch out for two years? Which factors matter the most?

We can tackle this question using the Kermack-McKendrick model of the spread of disease. (At the Data Community DC blog, I explain in detail how these equations work and how to make the proper analogies to use them to model viral marketing of a product.) In short, the total population is divided, into two subpopulations.

$S$ – The number of people susceptible to the disease but not infected (humans)
$I$ – The number of people who are actively infected with the disease (zombies a.k.a. walkers a.k.a. biters).

For now, we'll ignore recovery because nobody recovers from being a zombie. These two populations change in number over time as susceptible people become zombies, zombies are killed, and people are born and killed (without becoming zombies). Note that in the show, all humans are infected with the virus in a dormant state. For this model, "infection" means an active infection meaning that the human has become a zombie. This happens anytime a human dies by any means other than a gouge or shot to the brain. In terms of the model the human death rate then only refers to deaths where the human does not become a zombie.

The infection, birth, and death rates are given by the following parameters:

$\beta$ – The infection rate
$\alpha$ – Birth rate
$\mu$ – Death rate for humans (such that they do not become a zombie).
$\mu_z$ - Death rate for zombies

The equations for the populations of humans vs zombies are given by:

$dS / dt = −\beta S I + (\alpha–\mu) S$
$dI / dt = \beta S I – \mu_z I$.

Since these equations are non-linear, the best way to tackle them is by numerically integrating them and plotting the result.

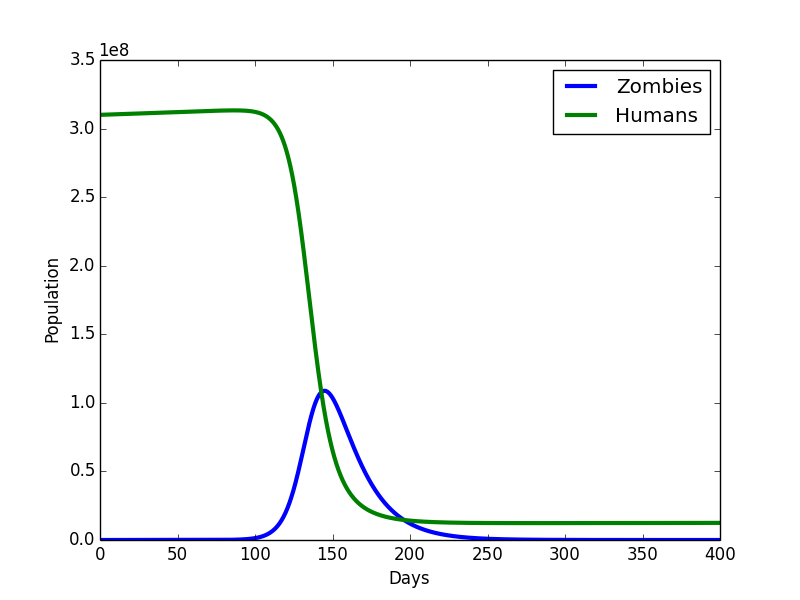
Let's say that the initial population is 310 million people (the population of the U.S.) and that the infection rate is 1 infection per zombie, per human, every 5 days. And let's assume initially, although it is not realistic, that birth and death rates haven't changed in the zombie apocalypse and remain at 14 per 1000 and 8 per 1000 per year respectively. Our zombie vs. human population then looks like:

That is, every human being in the U.S. becomes a zombie within 150 days. The zombies then dwindle out very slowly due to starvation and accidental brain gouges.

Now let's assume that zombie death rate is drastically higher such that zombies have an expected lifetime of only 30 days:

They still overwhelm the human population, though they never reach such high numbers all at once and die out much sooner.

Now, what if the expected lifetime of a zombie drops to two weeks and the human birth rate quadruples:

With this higher birth rate, we can survive the zombie apocalypse though the population would be mostly babies. It doesn't seem likely that such a population could continue to fight off the zombies.

Of course, in the Walking Dead, the zombie population overtakes humans within just a few weeks, leaving only a small fraction of the initial population. The only way this is possible is if the infection rate starts out very high and then drastically drops in the nick of time before the entire human population is eliminated. If the infection rate starts at 1 infection per zombie, per human, every day, and drops by a factor of 1000 on day 23, and the expected lifetime of a zombie is 200 days, we have: